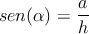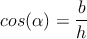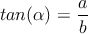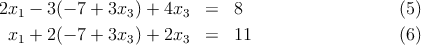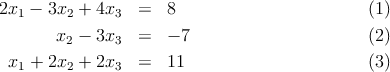
┐Cómo se definen las relaciones trigonométricas seno, coseno y tangente?
Respuestas:
- ┐Cómo aplico las leyes de los exponentes?
- anam = an+m
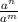 = an-m
= an-m
- 1 =
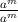 = am-m = a0
= am-m = a0
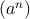 m = anm
m = anm
Ejemplo
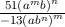 =?,
=?,
-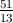
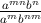 = -
= -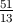 amnbna-mb-nm = -
amnbna-mb-nm = -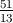 amn-mbn-nm =
-
amn-mbn-nm =
-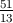 am(n-1)bn(1-m).
am(n-1)bn(1-m).
- ┐Cómo elevo al cuadrado el binomio a + b?
Se eleva al cuadrado como una multiplicación,
(a + b)2 = (a + b)(a + b) = aa + ab + ba + bb = a2 + 2ab + b2.
Se dice que es el cuadrado del primero más el doble del producto del primero por el segundo más el cuadrado del segundo.
Ejemplo
(3x2 + y)2 = 9x4 + 6x2y + y2. - ┐ A qué se refiere el profesor cuando nos pide que completemos un
cuadrado perfecto?
Lo que solicita, es pasar de un polinomio de la forma x2 + gx + e a la foma (x + h)2 + l donde g, e, h y l representan constantes.
Ejemplo
Completar el cuadrado perfecto de x2 + 2x - 7.
Lo que se puede hacer es tomar el coeficiente del término lineal (el que tiene solamente a la x) y dividirlo entre 2 para tener el término que sumará a la x dentro del binomio. En nuestro caso
x2 + 2x = x2 + 2x + (2∕2)2 - (2∕2)2 =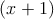 2 - 1, por lo tanto
2 - 1, por lo tanto
x2 + 2x - 7 =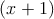 2 - 1 - 7 =
2 - 1 - 7 = 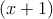 2 - 8.
2 - 8.
Ejemplo
Completar el cuadrado perfecto de x2 + x + .
.
x2 + x = x2 + x + (1∕2)2 - (1∕2)2 =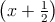 2 -
2 -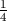 ,
,
x2 + x + =
= 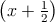 2 -
2 -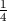 +
+  =
= 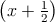 2 + 1.
2 + 1.
- ┐Qué significa resolver una ecuación cuadrática y cómo la resuelvo?
Una ecuación cuadrática tiene la forma
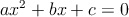
Resolver esta ecuación significa que debemos encontrar el valor de la x (de hecho son dos valores de x) que satisfacen la igualdad. Para encontrar la solución, primero se completará el cuadrado perfecto involucrado en esta expresión
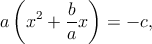
donde se ha supuesto que a≠0,
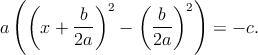
Luego se despeja la x,
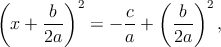
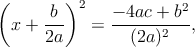
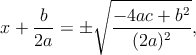
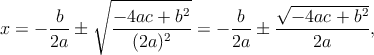
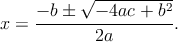
- Me piden que resuelva un sistema de ecuaciones de tres incógnitas, ┐Alguien
me puede ayudar? El sistema es:
Nota: Este problema fue tomado de The Chemistry Maths Book. Erich Steiner, Second Edition. OXFORD, 2008.
Una forma de abordar este problema es por el método de la sustitución. Por ejemplo, de la ecuación 2 obtenemos x2
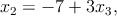
(4) y esta ecuación se sustituye en las ecuaciones 1 y 2 para obtener
Al hacer el álgebra necesaria se obtiene De la ecuación 8 se despeja x1,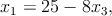
(9) para sustituir en la ecuación 7

(10) 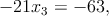
(11) 
(12) Finalmente, se sustituye este valor en la ecuación 9 para obtener x1 = 1 y en la ecuación 4 para obtener x2 = 2.
Voy a usar otro método, al cual se le conoce como la regla de Cramer, que te permitirá obtener la solución. Es un método algo tedioso pero es muy útil y si lo llevas a cabo con cuidado te ayudará siempre que lo necesites. Para asegurarnos primero que este sistema de ecuaciones tiene solución única evaluemos el determinante D el cual se obtiene de

Si resulta que D≠0 entonces tendremos una solución única del sistema. La manera de evaluar un determinante es de la siguiente manera
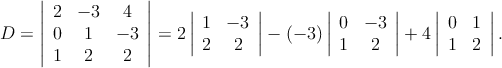
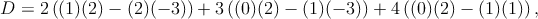
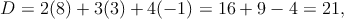
Como D≠0 entonces el sistema de ecuaciones admite de solución x1 = D1∕D, x2 = D2∕D y x3 = D3∕D. Donde D1, D2 y D3 son determinantes que se obtienen al sustituir cada columna del determinante con la columna que forma el lado derecho de cada ecuación del sistema de ecuaciones.
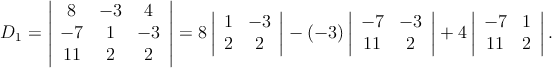
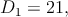
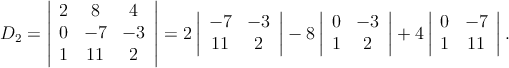
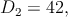

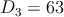
Por lo tanto,
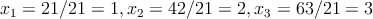
- ┐Cómo se definen las relaciones trigonométricas seno, coseno y tangente?
Estas relaciones se definen en términos de un triángulo rectángulo (necesariamente tiene un ángulo de 90 grados). Si en ese triángulo se toma un ángulo (diferente al ángulo recto), y lo nombramos α, entonces podemos nombrar a los lados del triángulo como:- Hipotenusa: Lado más largo del triángulo y es opuesto al ángulo recto. Lo denotaremos con la letra h.
- Cateto opuesto: Lado del triágulo que se encuentra opuesto al ángulo α. Lo denotaremos con la letra a.
- Cateto adyacente: Lado del triángulo que se encuentra junto al ángulo α. Lo denotaremos con la letra b.
Ya definidos los lados, se tiene que