4. Functionality

NWChem provides many methods to compute the properties of molecular and periodic systems using standard quantum mechanical descriptions of the electronic wavefunction or density. In addition, NWChem has the capability to perform classical molecular dynamics and free energy simulations. These approaches may be combined to perform mixed quantum-mechanics and molecular-mechanics simulations.

NWChem is available on almost all high performance computing platforms, workstations, PCs running LINUX, as well as clusters of desktop platforms or workgroup servers. NWChem development has been devoted to providing maximum efficiency on massively parallel processors. It achieves this performance on the 512 node IBM SP system in the EMSL's MSCF and on the 512 node CRAY T3E-900 system in the National Energy Research Scientific Computing Center. It has not been optimized for high performance on single processor desktop systems.

4.1 Molecular electronic structure

The following quantum mechanical methods are available to calculate energies and analytic first derivatives with respect to atomic coordinates. Second derivatives are computed by finite difference of the first derivatives.

• Self Consistent Field (SCF) or Hartree Fock (RHF, UHF, high-spin ROHF).
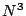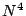• Gaussian Density Functional Theory (DFT), using many local and non-local exchange-correlation potentials (RHF or UHF) with formal $N^3$ and $N^4$ scaling.
• Spin-orbit DFT (SODFT), using many local and non-local exchange-correlation potentials (UHF).
• MP2 including semi-direct using frozen core and RHF and UHF reference.
• Complete active space SCF (CASSCF).

The following methods are available to compute energies only. First and second derivatives are computed by finite difference of the energies.

• CCSD, CCSD(T), CCSD+T(CCSD), with RHF reference.
• Selected-CI with second-order perturbation correction.
• MP2 fully-direct with RHF reference.
• Resolution of the identity integral approximation MP2 (RI-MP2), with RHF and UHF reference.

For all methods, the following operations may be performed:

• Single point energy
• Geometry optimization (minimization and transition state)
• Molecular dynamics on the fully ab initio potential energy surface
• Numerical first and second derivatives automatically computed if analytic derivatives are not available
• Normal mode vibrational analysis in cartesian coordinates
• ONIOM hybrid method of Morokuma and co-workers
• Generation of the electron density file for graphical display
• Evaluation of static, one-electron properties.
• Electrostatic potential fit of atomic partial charges (CHELPG method with optional RESP restraints or charge constraints)

For closed and open shell SCF and DFT:

• COSMO energies - the continuum solvation 'Conductor-Like Screening' Model of A. Klamt and G. Schuurmann to describe dielectric screening effects in solvents.

In addition, automatic interfaces are provided to

• The COLUMBUS multi-reference CI package
• The natural bond orbital (NBO) package
• Python

4.2 Relativistic effects

The following methods for including relativity in quantum chemistry calculations are available:

• The spin-free one-electron Douglas-Kroll approximation is available for all quantum mechanical methods and their gradients.
• Dyall's spin-free Modified Dirac Hamiltonian approximation is available for the Hartree-Fock method and its gradients.
• One-electron spin-orbit effects can be included via spin-orbit potentials. This option is available for DFT and its gradients, but has to be run without symmetry.

4.3 Pseudopotential plane-wave electronic structure

The following modules are available to compute the energy, minimize the geometry and perform ab initio molecular dynamics using pseudopotential plane-wave DFT.

• Fixed step length steepest descent
• Conuugate Gradient
• Car-Parrinello (extended Lagrangian dynamics)

With

• Vosko and PBE96 exchange-correlation potentials (restricted and unrestricted)
• (Gamma point) Periodic orthorhombic simulation cells for calculating molecules, liquids, crystals, and surfaces
• Aperiodic orthorhombic simulations cells for calculating molecules that are charged or highly polar
• Constant energy and constant temperature Car-Parrinello simulations
• Hamann and Troullier-Martins norm-conserving pseudopotentials with opt ional semicore corrections
• Modules to convert between small and large plane-wave expansions
• Interface to DRIVER, STEPPER, and VIB modules
• Mulliken analysis

4.4 Periodic system electronic structure

A module (Gaussian Approach to Polymers, Surfaces and Solids (GAPSS)) is available to compute energies by Gaussian Density Functional Theory (DFT) with many local and non-local exchange-correlation potentials.

4.5 Molecular dynamics

The following functionality is available for classical molecular simulations:

• Single configuration energy evaluation
• Energy minimization
• Molecular dynamics simulation
• Free energy simulation (multistep thermodynamic perturbation (MSTP) or multiconfiguration thermodynamic integration (MCTI) methods with options of single and/or dual topologies, double wide sampling, and separation-shifted scaling)

The classical force field includes:

• Effective pair potentials (functional form used in AMBER, GROMOS, CHARMM, etc.)
• First order polarization
• Self consistent polarization
• Smooth particle mesh Ewald (SPME)
• Twin range energy and force evaluation
• Periodic boundary conditions
• SHAKE constraints
• Consistent temperature and/or pressure ensembles

NWChem also has the capability to combine classical and quantum descriptions in order to perform:

• Mixed quantum-mechanics and molecular-mechanics (QM/MM) minimizations and molecular dynamics simulation , and
• Quantum molecular dynamics simulation by using any of the quantum mechanical methods capable of returning gradients.

4.6 Python

The Python programming language has been embedded within NWChem and many of the high level capabilities of NWChem can be easily combined and controlled by the user to perform complex operations.

4.7 Parallel tools and libraries (ParSoft)

• Global arrays (GA)
• Agregate Remote Memory Copy Interface (ARMCI)
• Linear Algebra (PeIGS) and FFT
• ParIO
• Memory allocation (MA)