The NWChem ET module uses the method of Corresponding Orbital Transformation to calculate the
electron transfer matrix element between ET reactant and product states,
![]() (
(![]() or
or ![]() in the literature). The only input required for the ET module is the
name of the files containing the open-shell (UHF or ODFT) MO vectors for the localized ET reactant and product states (
in the literature). The only input required for the ET module is the
name of the files containing the open-shell (UHF or ODFT) MO vectors for the localized ET reactant and product states (![]() and
and ![]() ).
).
The basis set used in the calculation of ![]() must be the same as the basis set used to calculate the MO vectors of
must be the same as the basis set used to calculate the MO vectors of
![]() and
and ![]() . The magnitude of
. The magnitude of ![]() depends on the amount of overlap between
depends on the amount of overlap between ![]() and
and ![]() ,
which is important to consider when choosing the basis set. Diffuse functions may be
necessary to fill in the overlap, particularly when the ET distance is long.
,
which is important to consider when choosing the basis set. Diffuse functions may be
necessary to fill in the overlap, particularly when the ET distance is long.
The magnitude of ![]() is a measurement of the degree of coupling between
is a measurement of the degree of coupling between ![]() and
and ![]() and,
therefore, the facility of the electron transfer. It's natural then that
and,
therefore, the facility of the electron transfer. It's natural then that ![]() is an important component in the expression for
the electron transfer rate:
is an important component in the expression for
the electron transfer rate:
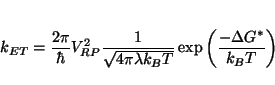 |
(27.1) |
Suggested references are listed below. The first reference gives a good basic description of Marcus' two-state ET model, and the appendix of the second reference details the method used in the ET module.
VECTORS [reactants] <string reactants_filename> VECTORS [products ] <string products_filename>
The VECTORS directive allows the user to specify the source
of the molecular orbital vectors for the ET reactant and product states.
This is required input, as no default filename will be set by the program.
In fact, this is the only required input in the ET module, although there are
other optional keywords described below.
<string (FOCK||NOFOCK) default FOCK>
This directive enables/disables the use of the NWChem's Fock matrix routine in the calculation of the two-electron portion of the ET Hamiltonian. Since the Fock matrix routine has been optimized for speed, accuracy and parallel performance, it is the most efficient choice.
The user can calculate the two-electron contribution to the ET Hamiltonian with another subroutine which may be more accurate for systems with a small number of basis functions, although it is slower.
<SWITCH2E <real switch2e default 1.0d-12>
In cases when the ET reactants and products are very weakly interacting (small ![]() ), the two-electron
contribution to the electronic coupling should not be calculated with the NWChem Fock matrix routine (see 10.7).
When
), the two-electron
contribution to the electronic coupling should not be calculated with the NWChem Fock matrix routine (see 10.7).
When ![]() is less than
is less than switch2e , the NOFOCK routine will be used for
the two electron contribution to the coupling (see 27.2).
TOL2E <real tol2e default max(10e-12,min(10e-7, S(RP)*10e-7 )>
The variable tol2e is used in determining the integral
screening threshold for the evaluation of the two-electron contribution to the Hamiltonian
between the electron transfer reactant and product states.
As a default, tol2e is set depending on the magnitude
of the overlap between the ET reactant and product states (![]() ), within the range 1.0d-12
), within the range 1.0d-12 ![]() 1.0d-7.
1.0d-7.
The input to specify the threshold explicitly within the ET
directive is, for example:
tol2e 1e-9
The following example is for a simple electron transfer reaction, ![]()
![]()
![]() .
The ET calculation is easy to execute, but it is crucial ET reactant and product
wavefunctions reflect localized states. This can be accomplished
using either a fragment guess (shown in the example, see 10.5.1), or a charged atomic
density guess (see 10.5.2).
Once the localized orbitals for the ET reactants have been calculated, you can use the
reactants' vectors with the
.
The ET calculation is easy to execute, but it is crucial ET reactant and product
wavefunctions reflect localized states. This can be accomplished
using either a fragment guess (shown in the example, see 10.5.1), or a charged atomic
density guess (see 10.5.2).
Once the localized orbitals for the ET reactants have been calculated, you can use the
reactants' vectors with the
REORDER keyword to move the electron from the first helium to the second see 27.1).
Example input :
#ET reactants: charge 1 scf doublet uhf vectors input fragment hep.mo he.mo output hea.mo # hep.mo are the vectors for He(+), # he.mo are the vectors for neutral He. end task scf #ET products: charge 1 scf doublet uhf vectors input hea.mo reorder 2 1 output heb.mo end task scf et vectors reactants hea.mo vectors products heb.mo end task scf etIt is important to verify the localization of the electron in the calculation of the vectors
hea.mo and heb.mo. To do this, carefully examine the Mulliken population
analysis. For the ET product state in the helium example, the Mulliken population
analysis looks like this:
Mulliken analysis of the total density
-------------------------------------
Atom Charge Shell Charges
----------- ------ -------------------------------------------------------
1 He 2 1.00 0.56 0.44
2 He 2 2.00 0.78 1.22
Atom Charge Shell Charges
----------- ------ -------------------------------------------------------
1 He 2 1.00 0.56 0.44
2 He 2 0.00 0.00 0.00
The Mulliken population analyses of the total and spin densities show that there is a single electron on
the first helium and a pair of electrons on the second helium.
Here is what the output looks like for this example:
Electron Transfer Calculation
-----------------------------
MO vectors for reactants: hea.mo
MO vectors for products : heb.mo
Electronic energy of reactants H(RR) -5.3402392824
Electronic energy of products H(PP) -5.3402392824
Reactants/Products overlap S(RP) -0.0006033839
Reactants/Products interaction energy:
-------------------------------------
One-electron contribution H1(RP) 0.0040314092
Beginning calculation of 2e contribution
Two-electron integral screening (tol2e) : 6.03E-11
Two-electron contribution H2(RP) -0.0007837138
Total interaction energy H(RP) 0.0032476955
Electron Transfer Coupling Energy |V(RP)| 0.0000254810
5.592 cm-1
0.000693 eV
0.016 kcal/mol
The overlap between the ET reactant and product states (![]() ) is small,
so the magnitude of the coupling between the states is also small.
If the fragment guess
or charged atomic density guess were not used, the spin density would be 0.5 on both He atoms, the overlap between
the ET reactant and product states would be
) is small,
so the magnitude of the coupling between the states is also small.
If the fragment guess
or charged atomic density guess were not used, the spin density would be 0.5 on both He atoms, the overlap between
the ET reactant and product states would be 100 % and an infinite
![]() would result.
would result.