A pseudopotential plane-wave (PSPW) module, which can perform Car-Parrinello simulations, is being implemented into the NWChem program package. This module complements the capabilities of the more traditional Gaussian function based approaches by including code which allows for the calculation of density functional theory total energies and forces with the technology based on plane-wave basis sets and pseudopotentials. Consistent with NWChem's philosophy this module is able to run on a variety of architectures, including parallel supercomputers.
The advantage of a PSPW method is that it has been shown to have an accuracy close to chemical accuracy for many applications, yet is still fast enough to treat systems containing hundreds of atoms. Another significant advantage is its ability to simulate dynamics on a ground state potential surface directly at run-time. This method's efficiency and accuracy make it a desirable first principles method of simulation in the study of complex molecular, liquid, and solid state systems. Applications for this first principles method include the calculation of free energies, search for global minima, explicit simulation of solvated molecules, and simulations of complex vibrational modes that cannot be described within the harmonic approximation.
Section 31.1 describes the tasks contained within the PSPW module. The RTDB entries and datafiles used by the PSPW module are described in section 31.2. Car-Parrinello output data files are described in section 31.2.9, and the minimization and Car-Parrinello algorithms are described in sections 31.3-31.4. Examples of how to setup and run a steepest descent simulation and a Car-Parrinello simulation are presented in sections 31.5-31.6. Finally in section 31.7 the capabilities and limitations of the PSPW module are discussed.
If you are a first time user of this module it is recommended that you skip the next five sections and proceed directly to the tutorials in sections 31.5-31.6.
All input to the PSPW Tasks is contained within the compound PSPW block,
PSPW ... END
To perform an actual calculation a TASK PSPW directive is used. The TASK
cg_pspw directive may also be used (see below). The format for the
TASK PSPW directive is the TASK directive followed by the
PSPW string, and after that an ![]() operation
operation![]() string is required. The
TASK PSPW directive for PSPW calculations is of the following form:
string is required. The
TASK PSPW directive for PSPW calculations is of the following form:
TASK PSPW [steepest_descent ||
conjugate_gradient ||
Car-Parrinello ||
psp_formatter ||
wavefunction_initializer ||
v_wavefunction_initializer ||
wavefunction_expander ||
psp_generator ||
(no default)]
Currently available tasks are listed. Note that unlike most
NWChem modules, the PSPW module does not contain an energy operation.
This means that there is no default operation and hence an operation must
always be specified.
PSPW tasks are of two types. The first type of task is used to setup or change needed data files for a PSPW simulation. Tasks of this type are psp_formatter, wavefunction_initializer, v_wavefunction_initializer, wavefunction_expander, and psp_generator. The second type of task is used to actually run a PSPW simulation. Tasks of this type are steepest_descent, and Car-Parrinello. The following subsections describe the input to these tasks.
The PSPW module is also interfaced to driver, stepper, and freqency task operations through the cg_pspw theory directive, see section 5.10.1. The PSPW conjugate_gradient sub-module is used in this interface. Specifically the following task operations are interafaced using the cg_pspw theory directive.
TASK cg_pspw energy #equivalent to TASK PSPW conjugate_gradient TASK cg_pspw gradient TASK cg_pspw optimize TASK cg_pspw saddle TASK cg_pspw freqencies TASK cg_pspw vib
The steepest_descent task is used to optimize the one-electron orbitals with respect to the total energy. In addition it can also be used to optimize geometries. This method is meant to be used for coarse optimization of the one-electron orbitals. A detailed description of the this method is described in section 31.3.1
Input to the steepest_descent simulation is contained within the steepest_descent sub-block.
PSPW
...
STEEPEST_DESCENT
...
END
...
END
To run a steepest_descent calculation the following directive is used:
TASK PSPW steepest_descentThe steepest_descent sub-block contains a great deal of input, including pointers to data, as well as parameter input. Listed below is the format of a STEEPEST_DESCENT sub-block.
PSPW
...
STEEPEST_DESCENT
CELL_NAME: <string cell_name>
[GEOMETRY_OPTIMIZE]
(FORMATTED_FILENAME: <string formatted_name> \
...)
INPUT_WAVEFUNCTION_FILENAME: <string input_wavefunctions default input_movecs>
OUTPUT_WAVEFUNCTION_FILENAME: <string output_wavefunctions default input_movecs>
FAKE_MASS: <real fake_mass default 400000.0>
TIME_STEP: <real time_step default 5.8>
LOOP: <integer inner_iteration outer_iteration default 10 1>
TOLERANCES: <real tole tolc tolr default 1.0d-9 1.0d-9 1.0d-4>
ENERGY_CUTOFF: <real ecut default (see input desciption)>
WAVEFUNCTION_CUTOFF: <real wcut default (see input description)>
EWALD_NCUT: <integer ncut default 1>
EWALD_RCUT: <real rcut default (see input description)>
EXCHANGE_CORRELATION: (Vosko || PBE96 default Vosko)
[MULLIKEN]
END
...
END
The following list describes the input for the STEEPEST_DESCENT
sub-block.
The conjugate_gradient task is used to optimize the one-electron orbitals with respect to the total energy. This method should be used for finer optimization. It is better to use the steepest_descent task when intitially optimizing the one-electron orbitals. A detailed description of the this method is described in section 31.3.2.
Input to the conjugate_gradient simulation is contained within the conjugate_gradient sub-block.
PSPW
...
CONJUGATE_GRADIENT
...
END
...
END
To run a conjugate_gradient calculation the following directive is used:
TASK PSPW conjugate_gradientThe conjugate_gradient sub-block contains a great deal of input, including pointers to data, as well as parameter input. Listed below is the format of a conjugate_gradient sub-block.
PSPW
...
CONJUGATE_GRADIENT
CELL_NAME: <string cell_name>
(FORMATTED_FILENAME: <string formatted_name> \
...)
INPUT_WAVEFUNCTION_FILENAME: <string input_wavefunctions default input_movecs>
OUTPUT_WAVEFUNCTION_FILENAME: <string output_wavefunctions default input_movecs>
[FAKE_MASS: <real fake_mass default 400000.0>]
[TIME_STEP: <real time_step default 5.8>]
LOOP: <integer inner_iteration outer_iteration default 10 1>
TOLERANCES: <real tole tolc default 1.0e-9 1.0e-9>
ENERGY_CUTOFF: <real ecut default (see input description)>
WAVEFUNCTION_CUTOFF: <real wcut default (see input description)>
EWALD_NCUT: <integer ncut default 1>]
EWALD_RCUT: <real rcut default (see input description)>
EXCHANGE_CORRELATION: (Vosko || PBE96 default Vosko)
[MULLIKEN]
END
...
END
The following list describes the input for the CONJUGATE_GRADIENT
sub-block.
Input to the Car-Parrinello simulation is contained within the Car-Parrinello sub-block.
PSPW
...
Car-Parrinello
...
END
...
END
To run a Car-Parrinello calculation the following directive is used:
TASK PSPW Car-ParrinelloThe Car-Parrinello sub-block contains a great deal of input, including pointers to data, as well as parameter input. Listed below is the format of a Car-Parrinello sub-block.
PSPW
...
Car-Parrinello
CELL_NAME: <string cell_name>
(FORMATTED_FILENAME: <string formatted_name> \
...)
INPUT_WAVEFUNCTION_FILENAME: <string input_wavefunctions default input_movecs>
OUTPUT_WAVEFUNCTION_FILENAME: <string output_wavefunctions default input_movecs>
INPUT_V_WAVEFUNCTION_FILENAME: <string input_v_wavefunctions default input_vmovecs>
OUTPUT_V_WAVEFUNCTION_FILENAME: <string output_v_wavefunctions default input_vmovecs>
FAKE_MASS: <real fake_mass default default 1000.0>
TIME_STEP: <real time_step default 5.0>
LOOP: <integer inner_iteration outer_iteration default 10 1>
SCALING: <real scale_c scale_r default 1.0 1.0>
ENERGY_CUTOFF: <real ecut default (see input description)>
WAVEFUNCTION_CUTOFF: <real wcut default (see input description)>
EWALD_NCUT: <integer ncut default 1>
EWALD_RCUT: <real rcut default (see input description)>
EXCHANGE_CORRELATION: (Vosko || PBE96 default Vosko)
[Nose-Hoover: <real Period_electron Temperature_electrion Period_ion Temperature_ion
default 100.0 298.15 100.0 298.15>]
XYZ_FILENAME: <string xyz_filename default XYZ>
EMOTION_FILENAME: <string emotion_filename default EMOTION>
HMOTION_FILENAME: <string hmotion_filename default HMOTION>
OMOTION_FILENAME: <string omotion_filename default OMOTION>
EIGMOTION_FILENAME: <string eigmotion_filename default EIGMOTION>
ION_MOTION_FILENAME: <string ion_motion_filename default MOTION>
END
...
END
The following list describes the input for the Car-Parrinello
sub-block.
Input to the PSP_FORMATTER task is contained within the PSP_FORMATTER sub-block.
PSPW
...
PSP_FORMATTER
...
END
...
END
To run a PSP_FORMATTER calculation the following directive is used:
TASK PSPW PSP_FORMATTERListed below is the format of a PSP_FORMATTER sub-block.
PSPW
...
PSP_FORMATTER
CELL_NAME: <string cell_name>
PSP_FILENAME: <string psp_name>
FORMATTED_FILENAME: <string formatted_name>
LOCP: (s||p||d||f||g default (see input description))
LMAX: (s||p||d||f||g default (see input description))
end
...
END
The following list describes the input for the PSP_FORMATTER
sub-block.
PSPW
...
WAVEFUNCTION_INITIALIZER
...
END
...
END
To run a WAVEFUNCTION_INITIALIZER calculation the following directive
is used:
TASK PSPW WAVEFUNCTION_INITIALIZERListed below is the format of a WAVEFUNCTION_INITIALIZER sub-block.
PSPW
...
WAVEFUNCTION_INITIALIZER
CELL_NAME: <string cell_name>
WAVEFUNCTION_FILENAME: <string wavefunction_name default input_movecs>
(RESTRICTED||UNRESTRICTED)
if (RESTRICTED)
RESTRICTED_ELECTRONS: <integer restricted electrons>
if (UNRESTRICTED)
UP_ELECTRONS: <integer up_electrons>
DOWN_ELECTRONS: <integer down_electrons>
END
...
END
The following list describes the input for the WAVEFUNCTION_INITIALIZER
sub-block.
For backwards compatibility, the input to the WAVEFUNCTION_INITIALIZER sub-block can also be of the form
PSPW
...
WAVEFUNCTION_INITIALIZER
CELL_NAME: <string cell_name>
WAVEFUNCTION_FILENAME: <string wavefunction_name default input_movecs>
(RESTRICTED||UNRESTRICTED)
[UP_FILLING: <integer up_filling>
[0 0 0 0]
{<integer kx ky kz> (-2||-1||1||2)}]
[DOWN_FILLING: <integer down_filling>
[0 0 0 0]
{<integer kx ky kz> (-2||-1||1||2)}]
END
...
END
where
The values for the planewave
![]() are used to represent whether
the specified planewave is a cosine or a sine function, in addition
random noise can be added to these base functions. That is
are used to represent whether
the specified planewave is a cosine or a sine function, in addition
random noise can be added to these base functions. That is ![]() represents a cosine function, and
represents a cosine function, and ![]() represents a sine function.
The
represents a sine function.
The ![]() and
and ![]() values are used to represent a cosine function with
random components added and a sine function with random components
added respectively.
values are used to represent a cosine function with
random components added and a sine function with random components
added respectively.
PSPW
...
V_WAVEFUNCTION_INITIALIZER
...
END
...
END
To run a V_WAVEFUNCTION_INITIALIZER calculation the following directive
is used:
TASK PSPW WAVEFUNCTION_INITIALIZERListed below is the format of a V_WAVEFUNCTION_INITIALIZER sub-block.
PSPW
...
V_WAVEFUNCTION_INITIALIZER
V_WAVEFUNCTION_FILENAME: <string v_wavefunction_name default input_vmovecs>
CELL_NAME: <string cell_name>
(RESTRICTED||UNRESTRICTED)
UP_FILLING: <integer up_filling>
DOWN_FILLING: <integer down_filling>
END
...
END
The following list describes the input for the V_WAVEFUNCTION_INITIALIZER
sub-block.
PSPW
...
WAVEFUNCTION_EXPANDER
...
END
...
END
To run a WAVEFUNCTION_EXPANDER calculation the following directive
is used:
TASK PSPW WAVEFUNCTION_EXPANDERListed below is the format of a WAVEFUNCTION_EXPANDER sub-block.
PSPW
...
WAVEFUNCTION_EXPANDER
OLD_WAVEFUNCTION_FILENAME: <string old_wavefunction_name default input_movecs>
NEW_WAVEFUNCTION_FILENAME: <string new_wavefunction_name default input_movecs>
NEW_NGRID: <integer na1 na2 na3>
END
...
END
The following list describes the input for the WAVEFUNCTION_EXPANDER
sub-block.
A one-dimensional pseudopotential code has been integrated into NWChem. This code allows the user to modify and develop pseudopotentials. Currently, only the Hamann and Troullier-Martins norm-conserving pseudopotentials can be generated. This file can then be used by the pseudopotential_formatter task to generate a formatted pseudopotential file. Input to the PSP_GENERATOR task is contained within the PSP_GENERATOR sub-block.
PSPW
...
PSP_GENERATOR
...
END
...
END
To run a PSP_GENERATOR calculation the following directive
is used:
TASK PSPW PSP_GENERATORListed below is the format of a PSP_GENERATOR sub-block.
PSPW
...
PSP_GENERATOR
PSEUDOPOTENTIAL_FILENAME: <string psp_name>
ELEMENT: <string element>
CHARGE: <real charge>
MASS_NUMBER: <real mass_number>
ATOMIC_FILLING: <integer ncore nvalence>
( (1||2||...) (s||p||d||f||...) <real filling> \
...)
[CUTOFF: <integer lmax>
( (s||p||d||f||g) <real rcut>\
...)
]
PSEUDOPOTENTIAL_TYPE: (TROULLIER-MARTINS || HAMANN default HAMANN)
SOLVER_TYPE: (PAULI || SCRHODINGER default PAULI)
EXCHANGE_TYPE: (dirac || PBE96 default DIRAC)
CORRELATION_TYPE: (VOSKO || PBE96 default VOSKO)
[SEMICORE_RADIUS: <real rcore>]
end
...
END
The following list describes the input for the PSP_GENERATOR
sub-block.
For example to define a pseudopotential
for the Neon atom in the
![]() state
could have the block
state
could have the block
ATOMIC_FILLING: 1 2
1 s 2.0 #core state - 1s^2
2 s 2.0 #valence state - 2s^2
2 p 6.0 #valence state - 2p^6
for a pseudopotential with a
ATOMIC_FILLING: 3 0
1 s 2.0 #core state
2 s 2.0 #core state
2 p 6.0 #core state
could be used for a pseudopotential with no valence electrons.
For example to define a softened Hamann pseudopotential for Carbon would be
ATOMIC_FILLING: 1 2 1 s 2.0 2 s 2.0 2 p 2.0 CUTOFF: 2 s 0.8 p 0.85 d 0.85while a similarly softened Troullier-Marting pseudopotential for Carbon would be
ATOMIC_FILLING: 1 2 1 s 2.0 2 s 2.0 2 p 2.0 CUTOFF: 2 s 1.200 p 1.275 d 1.275
The implmentation in the PSPW module defines the semi-core denisty,
![]() in terms of
the core density,
in terms of
the core density, ![]() , by using the sixth-order polynomial
, by using the sixth-order polynomial
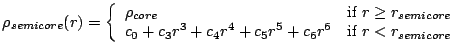 |
(31.1) |
PSPW
...
SIMULATION_CELL
CELL_NAME: <string name>
BOUNDRY_CONDITIONS: (periodic || aperiodic)
LATTICE_VECTORS:
<real a1.x a1.y a1.z>
<real a2.x a2.y a2.z>
<real a3.x a3.y a3.z>
NGRID: <integer na1 na2 na3>
END
...
END
Basically, the user needs to enter the dimensions, gridding and boundry
conditions of the simulation cell. The following list describes the
input in detail.
To perform Mulliken analysis information is needed from one-dimensional pseudopotential files. In-order to facilitate the transfer of this information to the simulation the ANALYSIS sub-block is used to exract the necessary information and put it into the RTDB.
PSPW
...
ANALYSIS
(psp_filename: <string psp_name> \
...)
END
...
END
Basically, the user needs to enter each pseudopotential used in the simulation.
The data stored in the one-dimensional pseudopotential file is
character*2 element :: element name integer charge :: valence charge of ion real mass :: mass of ion integer lmax :: maximum angular component real rcut(lmax) :: cutoff radii used to define pseudopotentials integer nr :: number of points in the radial grid real dr :: linear spacing of the radial grid real r(nr) :: one-dimensional radial grid real Vpsp(nr,lmax) :: one-dimensional pseudopotentials real psi(nr,lmax) :: one-dimensional pseudowavefunctions real r_semicore :: semicore radius real rho_semicore(nr) :: semicore densityand the format of it is:
[line 1: ] element [line 2: ] charge mass lmax [line 3: ] (rcut(l), l=1,lmax) [line 4: ] nr dr [line 5: ] r(1) (Vpsp(1,l), l=1,lmax) [line 6: ] .... [line nr+4: ] r(nr) (Vpsp(nr,l), l=1,lmax) [line nr+5: ] r(1) (psi(1,l), l=1,lmax) [line nr+6: ] .... [line 2*nr+4:] r(nr) (psi(nr,l), l=1,lmax) [line 2*nr+5:] r_semicore if (r_semicore read) then [line 2*nr+6:] r(1) rho_semicore(1) [line 2*nr+7:] .... [line 3*nr+5:] r(nr) rho_semicore(nr) end if
[line 1: ] n_ion [line 2: ] do ii=1,n_ion [line 2+ii: ] atom_name(ii), x(ii),y(ii),z(ii),vx(ii),vy(ii),vz(ii) end do [line n_ion+3 ] n_nion do ii=1,n_ion [line n_ion+3+ii: ] atom_name(ii), x(ii),y(ii),z(ii), vx(ii),vy(ii),vz(ii) end do [line 2*n_ion+4: ] ....
[line 1: ] it_out, n_ion, omega [line 2: ] time do ii=1,n_ion [line 2+ii: ] x(ii),y(ii),z(ii), vx(ii),vy(ii),vz(ii) end do [line n_ion+3 ] time do do ii=1,n_ion [line n_ion+3+ii: ] x(ii),y(ii),z(ii), vx(ii),vy(ii),vz(ii) end do [line 2*n_ion+4: ] ....
[line 1: ] time, E1,E2,E3,E4,E5,E6,E7,E8, (E9,E10, if Nose-Hoover) [line 2: ] ...
[line 1: ] time [line 2: ] ms,ne(ms),ne(ms) do i=1,ne(ms) [line 2+i: ] (hml(i,j), j=1,ne(ms) end do [line 3+ne(ms): ] time [line 4+ne(ms): ] ....
[line 1: ] time, (eig(i), i=1,number_orbitals) [line 2: ] ...
In this section the algorithms for steepest_descent and conjugate_gradient methods that are used to minimize the DFT energy functional are presented. First is the the steepest descent method without line minimization. This method is slow, but doesn't require line minimization. Second is the recent method developed by Edelman, Arias, and Smith. These researchers have developed methods for performing line minimizations on the constrained space used in the DFT energy functional (A. Edelman, T. Arias, and S.T. Smith, Siam J. Matrix Anal. Appl., 20,303, (1998)).
To minimize the DFT energy functional with respect to
![]() we define the the auxiliary functional,
we define the the auxiliary functional, ![]() , which takes into account
the orthonormality constraints.
, which takes into account
the orthonormality constraints.
The steepest descent minimization procedure without line minimization
is then
The ion positions can also be minimized using a fixed step minimization
procedure.
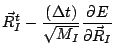 |
(31.5) |
To find the matrix
![]() we impose the orthonormality
constraint on
we impose the orthonormality
constraint on
![]() to obtain the
matrix Riccatti equation
(to simplify the following equations we define the following symbol
to obtain the
matrix Riccatti equation
(to simplify the following equations we define the following symbol
![]() )
)
where
![]() and the matrices
and the matrices
![]() ,
, ![]() , and
, and ![]() are given by
are given by
![$\displaystyle \int d\vec{r}
\left[\psi_{i,\sigma}^{t}(\vec{r})
- \alpha
\left( ...
...)
- \alpha
\left( \frac{\delta E}{\delta \psi_{j,\sigma}^{*}}
\right)_t
\right]$](img292.gif) |
(31.7) | ||
![$\displaystyle \int d\vec{r}
\left[\psi_{i,\sigma}^{t}(\vec{r})
\right]^{*}
\lef...
...)
- \alpha
\left( \frac{\delta E}{\delta \psi_{j,\sigma}^{*}}
\right)_t
\right]$](img294.gif) |
(31.8) | ||
![$\displaystyle \int d\vec{r}
\left[\psi_{i,\sigma}^{t}(\vec{r})
\right]^{*}
\left[\psi_{j,\sigma}^{t}(\vec{r})
\right]$](img296.gif) |
(31.9) |
To solve the Riccatti equation an iterative solution is setup by rewriting
Eq. 31.6 in the following form.
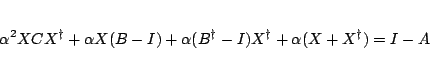 |
(31.10) |
| (31.11) |
Minimizing the DFT energy functional with a non-linear conjugate gradient algorithm requires an algorithm for minimizing along a search direction or line. However, the equation for a line (or search direction) in the DFT minimization problem is complicated by the fact that the energy functional is subject to orthonormality constraints. Furthermore, the orthonormality constraints complicate the conjugate gradient's algorithm for generating the current search direction by using a linear combination of the current gradient and the previous search direction, since the previous search direction must be parallel transported to the current search point.
These orthonormality constraint problems
have been investigated and solved for by Edelman et al
(A. Edelman, T. Arias, and S.T. Smith, Siam J. Matrix Anal. Appl.,
20,303, (1998)).
They recognized that the orthonormal Kohn-Sham
orbitals
![]() belong to a quotient space called a Grassmann manifold.
Using the properties of the Grassmann manifold they
developed an equation for a line (or geodesic) which
conserves orthonormality, as well as
a conjugate gradient procedure for generating the current search direction on this
constrained space.
belong to a quotient space called a Grassmann manifold.
Using the properties of the Grassmann manifold they
developed an equation for a line (or geodesic) which
conserves orthonormality, as well as
a conjugate gradient procedure for generating the current search direction on this
constrained space.
Following Edelman et al we write
![]() in terms of the orthonormal basis
in terms of the orthonormal basis
![]() .
.
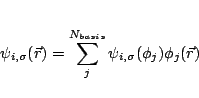 |
(31.14) |
![\begin{displaymath}
Y_{\uparrow}=\left[\begin{array}{rrrr}
\psi_{1,\uparrow}(\p...
...{N_{\uparrow},\uparrow}(\phi_{N_{basis}})
\end{array} \right]
\end{displaymath}](img314.gif) |
(31.15) |
![\begin{displaymath}
Y_{\downarrow}=\left[\begin{array}{rrrr}
\psi_{1,\downarrow...
...\downarrow},\downarrow}(\phi_{N_{basis}})
\end{array} \right]
\end{displaymath}](img315.gif) |
(31.16) |
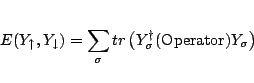 |
(31.17) |
 31.1).
31.1).
In this work Algorithm 31.1 (see below) is the
conjugate gradient
algorithm that is used to minimize the DFT energy functional
![]() . What makes this
algorithm different from a standard
Polak-Ribière conjugate gradient algorithm
is that a line search on a Euclidean space
. What makes this
algorithm different from a standard
Polak-Ribière conjugate gradient algorithm
is that a line search on a Euclidean space
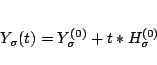
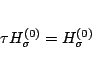
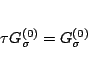
Given
![]() such that
such that
![]() ,
,
Compute
![]()
Set
![]() .
Find the compact singular value decompositions of
.
Find the compact singular value decompositions of
![]() Minimize
Minimize
![]() along the
geodesic lines derived by Edelman et al for the
Grassmann Manifold
along the
geodesic lines derived by Edelman et al for the
Grassmann Manifold
Car and Parrinello developed a unified scheme for doing ab initio molecular dynamics by combining the motion of the ion cores and a fictacious motion for the Kohn-Sham orbitals of density-functional theory (R. Car and M. Parrinello, Phys. Rev. Lett. 55, 2471, (1985)). At the heart of this method they introduced a fictacious kinetic energy functional for the Kohn-Sham orbitals.
Given this kinetic energy the constrained equations of motion are found
by taking the first variation of the auxiliary Lagrangian.
Which generates a dynamics for the wavefunctions and atoms positions through the constrained equations of motion:
where ![]() is the fictitious mass for the electronic degrees of freedom and
are the ionic masses.
The adjustable parameter
is the fictitious mass for the electronic degrees of freedom and
are the ionic masses.
The adjustable parameter ![]() is used to
describe the relative rate at which the wavefunctions change with time.
is used to
describe the relative rate at which the wavefunctions change with time.
![]() are the
Lagrangian multipliers for the orthonormalization of the single-particle
orbitals
.
They are defined by the orthonormalization constraint conditions
and can be rigorously found.
However, the equations of motion for the Lagrange multipliers
depend on the specific algorithm used to integrate
Eqs. 31.24-31.25.
are the
Lagrangian multipliers for the orthonormalization of the single-particle
orbitals
.
They are defined by the orthonormalization constraint conditions
and can be rigorously found.
However, the equations of motion for the Lagrange multipliers
depend on the specific algorithm used to integrate
Eqs. 31.24-31.25.
For this method to give ionic motions that are physically meaningful the kinetic energy of the Kohn-Sham orbitals must be relatively small when compared to the kinetic energy of the ions. There are two ways where this criterion can fail. First, the numerical integrations for the Car-Parrinello equations of motion can often lead to large relative values of the kinetic energy of the Kohn-Sham orbitals relative to the kinetic energy of the ions. This kind of failure is easily fixed by requiring a more accurate numerical integration, i.e. use a smaller time step for the numerical integration. Second, during the motion of the system a the ions can be in locations where there is an Kohn-Sham orbital level crossing, i.e. the density-functional energy can have two states that are nearly degenerate. This kind of failure often occurs in the study of chemical reactions. This kind of failure is not easily fixed and requires the use of a more sophisticated density-functional energy that accounts for low-lying excited electronic states.
Eqs. 31.24-31.25 integrated using the Verlet algorithm results in
In this molecular dynamic procedure we have to know variational derivative
![]() and the matrix
and the matrix
![]() .
The variational derivative
.
The variational derivative
![]() can be analytically found and is
can be analytically found and is
To find the matrix
![]() we impose the orthonormality
constraint on
we impose the orthonormality
constraint on
![]() to obtain a
matrix Riccatti equation, and then Riccatti equation is solved by an iterative
solution (see section 31.3.1).
to obtain a
matrix Riccatti equation, and then Riccatti equation is solved by an iterative
solution (see section 31.3.1).
Nose-Hoover Thermostats for the electrons and ions can also be added to the
Car-Parrinello simulation. In this type of simulation thermostats variables and
are added to the simulation by adding the auxillary energy functionals to the total energy.
| (31.28) | |||
| (31.29) |
In these equations, the average kinetic energy for the ions is
| (31.30) |
| (31.31) |
Blöchl and Parrinello suggested that the choice of mass parameters,
, and should be made such that the period of oscillating thermostats
should be chosen larger than the typical time scale for the dynamical events of
interest but shorter than the simulation time.
| (31.32) | |||
| (31.33) |
In this section we show how to setup and run a steepest descent simulation followed by a conjugate gradient simulation to optimize the one-electron orbitals with respect to the total energy for a NaCl molecule. It is practical to start most simulation in such a tandem fashion because the conjugate gradient optimizer does not work well when the one-electron orbitals are far from minimized.
Before running a steepest_descent or conjugate_gradient simulation several files and RTDB structures must be defined or initialized. Specifically, the user is required to have defined:
In the following tutorial we show the input needed to find an energy for an NaCl molecule. In this example default Hamann pseudopotentials are used for Na and Cl, the exchange correlation functional is LSDA, and the cutoff energy is 12 au. This example input deck can be found in the nwchem source tree in the file: nwchem/examples/pspw/NaCl.nw
...
geometry units au
Na 2.23 0.0 0.0
Cl -2.23 0.0 0.0
end
...
...
PSPW
PSP_GENERATOR
pseudopotential_filename: Na.psp
element: Na
charge: 11.0
mass_number: 23.0
solver_type: pauli
pseudopotential_type: hamann
atomic_filling: 3 1
1 s 2.0
2 s 2.0
2 p 6.0
3 s 1.0
END
END
task PSPW PSP_GENERATOR
...
...
PSPW
PSP_GENERATOR
pseudopotential_filename: Cl.psp
element: Cl
charge: 17.0
mass_number: 35.0
solver_type: pauli
pseudopotential_type: hamann
atomic_filling: 3 2
1 s 2.0
2 s 2.0
2 p 6.0
3 s 2.0
3 p 5.0
END
END
task PSPW PSP_GENERATOR
...
...
PSPW
SIMULATION_CELL
cell_name: small
boundry_conditions: periodic
lattice_vectors:
20.0 0.0 0.0
0.0 20.0 0.0
0.0 0.0 20.0
ngrid: 32 32 32
END
END
...
...
PSPW
PSP_FORMATTER
cell_name: small
psp_name: Na.psp
formatted_name: Na.vpp
END
END
task PSPW PSP_FORMATTER
...
...
PSPW
PSP_FORMATTER
cell_name: small
psp_name: Cl.psp
formatted_name: Cl.vpp
END
END
task PSPW PSP_FORMATTER
...
...
PSPW
WAVEFUNCTION_INITIALIZER
cell_name: small
unrestricted
up_electrons: 4
down_electrons: 4
wavefunction_filename: NaCl.small.00.elc
END
END
task PSPW WAVEFUNCTION_INTITALIZER
...
...
PSPW
STEEPEST_DESCENT
cell_name: small
formatted_filename: Na.vpp
formatted_filename: Cl.vpp
input_wavefunction_filename: NaCl.small.00.elc
output_wavefunction_filename: NaCl.small.00.elc
fake_mass: 400000.0d0
time_step: 51.8d0
loop: 10 100
tolerances: 1.0d-4 1.0d-4 1.0d-4
energy_cutoff: 21.0d0
wavefunction_cutoff: 21.0d0
END
END
task PSPW STEEPEST_DESCENT
...
...
PSPW
CONJUGATE_GRADIENT
cell_name: small
formatted_filename: Na.vpp
formatted_filename: Cl.vpp
input_wavefunction_filename: NaCl.small.00.elc
output_wavefunction_filename: NaCl.small.00.elc
loop: 25 10
tolerances: 1.0d-9 1.0d-9
energy_cutoff: 21.0d0
wavefunction_cutoff: 21.0d0
Mulliken
END
ANALYSIS
psp_name: Na.psp
psp_name: Cl.psp
END
END
task PSPW CONJUGATE_GRADIENT
...
In this section we show how to perform a Car-Parrinello molecular dynamic simulation for an NaCl molecule. As with the example in the previous tutorial, this example uses default Hamann pseudopotentials for Na and Cl, LSDA exchange correlation functional, and a cutoff energy of 12 au.
Before running a PSPW Car-Parrinello simulation the system should be on the Born-Oppenheimer surface, i.e. the one-electron orbitals should be minimized with respect to the total energy using steepest descent and conjugate gradient simulations(see section 31.5).
Continuning where we left off in section 31.5 we now continue the simulation to run a MD simulation of an NaCl molecule. This example input deck can be found in the nwchem source tree in the file: nwchem/examples/pspw/NaCl-md.nw
...
PSPW
V_WAVEFUNCTION_INITIALIZER
cell_name: small
unrestricted
up_filling: 4
down_filling: 4
v_wavefunction_filename: NaCl.small.00.velc
END
END
task PSPW WAVEFUNCTION_INTITALIZER
...
PSPW
Car-Parrinello
cell_name: small
formatted_filename: Na.vpp
formatted_filename: Cl.vpp
input_wavefunction_filename: NaCl.small.00.elc
output_wavefunction_filename: NaCl.small.01.elc
v_input_wavefunction_filename: NaCl.00.velc
v_output_wavefunction_filename: NaCl.01.velc
fake_mass: 800.0d0
time_step: 5.0d0
loop: 10 100
scaling: 1.0d0 1.0d0
energy_cutoff: 21.0d0
wavefunction_cutoff: 21.0d0
END
END
task PSPW Car-Parrinello
...
Questions and encountered problems should be reported to nwchem-support@emsl.pnl.gov or to Eric J. Bylaska, Eric.Bylaska@pnl.gov