11. DFT for Molecules (DFT)

The NWChem density functional theory (DFT) module uses the Gaussian basis set approach to compute closed shell and open shell densities and Kohn-Sham orbitals in the:

• local density approximation (LDA),
• non-local density approximation (NLDA),
• local spin-density approximation (LSD),
• non-local spin-density approximation (NLSD), and
• any empirical mixture of local and non-local approximations (including exact exchange).

The formal scaling of the DFT computation can be reduced by choosing to use auxiliary Gaussian basis sets to fit the charge density (CD) and/or fit the exchange-correlation (XC) potential.

DFT input is provided using the compound DFT directive

  DFT
    ...
  END

The actual DFT calculation will be performed when the input module encounters the TASK directive (Section 5.10).

  TASK DFT

Once a user has specified a geometry and a Kohn-Sham orbital basis set the DFT module can be invoked with no input directives (defaults invoked throughout). There are sub-directives which allow for customized application; those currently provided as options for the DFT module are:

  VECTORS [[input] (<string input_movecs default atomic>) || \
                   (project <string basisname> <string filename>)] \
           [swap [alpha||beta] <integer vec1 vec2> ...] \
           [output <string output_filename default input_movecs>] \


  XC [[acm] [b3lyp] [beckehandh] [pbe0]\
     [becke97]  [becke97-1] [becke97-2] [becke98] [hcth] [hcth120] [hcth147]\
      [h407] [becke97gga1] [mpw91] [mpw1k] [xft97] [cft97] [ft97] [xpkzb99] \
      [HFexch <real prefactor default 1.0>] \
      [becke88 [nonlocal] <real prefactor default 1.0>] \
      [xperdew91 [nonlocal] <real prefactor default 1.0>] \
      [xpbe96 [nonlocal] <real prefactor default 1.0>] \
      [gill96 [nonlocal] <real prefactor default 1.0>] \
      [lyp <real prefactor default 1.0>] \
      [perdew81 <real prefactor default 1.0>] \
      [perdew86 [nonlocal] <real prefactor default 1.0>] \
      [perdew91 [nonlocal] <real prefactor default 1.0>] \
      [cpbe96 [nonlocal] <real prefactor default 1.0>] \
      [pw91lda <real prefactor default 1.0>] \
      [slater <real prefactor default 1.0>] \
      [vwn_1 <real prefactor default 1.0>] \
      [vwn_2 <real prefactor default 1.0>] \
      [vwn_3 <real prefactor default 1.0>] \
      [vwn_4 <real prefactor default 1.0>] \
      [vwn_5 <real prefactor default 1.0>] \
      [vwn_1_rpa <real prefactor default 1.0>]]


  CONVERGENCE [[energy <real energy default 1e-7>] \
               [density <real density default 1e-5>] \
               [gradient <real gradient default 5e-4>] \
               [dampon <real dampon default 0.0>] \
               [dampoff <real dampoff default 0.0>] \
               [diison <real diison default 0.0>] \
               [diisoff <real diisoff default 0.0>] \
               [levlon <real levlon default 0.0>] \
               [levloff <real levloff default 0.0>] \
               [ncydp <integer ncydp default 2>] \
               [ncyds <integer ncyds default 30>] \
               [ncysh <integer ncysh default 30>] \
               [damp <integer ndamp default 0>] [nodamping] \
               [diis [nfock <integer nfock default 10>]] \
               [nodiis] [lshift <real lshift default 0.5>] \
               [nolevelshifting] \
               [hl_tol <real hl_tol default 0.1>] \
               [rabuck [n_rabuck <integer n_rabuck default 25>]]


  GRID [(xcoarse||coarse||medium||fine||xfine) default medium] \
       [(gausleg||lebedev ) default lebedev ] \
       [(old||new) default new ] \
       [(becke||erf1||erf2||ssf) default erf1] \
       [(euler||mura||treutler) default mura] \
       [rm <real rm default 2.0>]
        

  TOLERANCES [[tight] [tol_rho <real tol_rho default 1e-10>] \
              [accCoul <integer accCoul default 8>] \
              [radius <real radius default 25.0>]]


  DECOMP
  ODFT
  DIRECT
  INCORE
  ITERATIONS <integer iterations default 30>
  MAX_OVL
  MULLIKEN
  MULT <integer mult default 1>
  NOIO
  PRINT||NOPRINT

The following sections describe these keywords and optional sub-directives that can be specified for a DFT calculation in NWChem.

11.1 Specification of Basis Sets for the DFT Module

The DFT module requires at a minimum the basis set for the Kohn-Sham molecular orbitals. This basis set must be in the default basis set named "ao basis", or it must be assigned to this default name using the SET directive (see Section 5.7).

In addition to the basis set for the Kohn-Sham orbitals, the charge density fitting basis set can also be specified in the input directives for the DFT module. This basis set is used for the evaluation of the Coulomb potential in the Dunlap scheme^11.1. The charge density fitting basis set must have the name "cd basis". This can be the actual name of a basis set, or a basis set can be assigned this name using the SET directive, as described in Section 5.7. If this basis set is not defined by input, the $O(N^4)$ exact Coulomb contribution is computed.

The user also has the option of specifying a third basis set for the evaluation of the exchange-correlation potential. This basis set must have the name "xc basis". If this basis set is not specified by input, the exchange contribution (XC) is evaluated by numerical quadrature. In most applications, this approach is efficient enough, so the "xc basis" basis set is not generally required.

For the DFT module, the input options for defining the basis sets in a given calculation can be summarized as follows;

• "ao basis" - Kohn-Sham molecular orbitals; required for all calculations
• "cd basis" - charge density fitting basis set; optional, but recommended for evaluation of the Coulomb potential
• "xc basis" - exchange-correlation (XC) fitting basis set; optional, and usually not recommended

11.2 VECTORS and MAX_OVL -- KS-MO Vectors

The VECTORS directive is the same as that in the SCF module (Section 10.5). Currently, the LOCK keyword is not supported by the DFT module, however the directive

  MAX_OVL

has the same effect.

11.3 XC and DECOMP -- Exchange-Correlation Potentials

  XC [[acm] [b3lyp] [beckehandh] [pbe0]\
     [becke97]  [becke97-1] [becke97-2] [becke98] [hcth] [hcth120] [hcth147] \
      [hcth407] [becke97gga1] [optx] [hcthp14] [mpw91] [mpw1k] [xft97] [cft97] [ft97]\
      [HFexch <real prefactor default 1.0>] \
      [becke88 [nonlocal] <real prefactor default 1.0>] \
      [xperdew91 [nonlocal] <real prefactor default 1.0>] \
      [xpbe96 [nonlocal] <real prefactor default 1.0>] \
      [gill96 [nonlocal] <real prefactor default 1.0>] \
      [lyp <real prefactor default 1.0>] \
      [perdew81 <real prefactor default 1.0>] \
      [perdew86 [nonlocal] <real prefactor default 1.0>] \
      [perdew91 [nonlocal] <real prefactor default 1.0>] \
      [cpbe96 [nonlocal] <real prefactor default 1.0>] \
      [pw91lda <real prefactor default 1.0>] \
      [slater <real prefactor default 1.0>] \
      [vwn_1 <real prefactor default 1.0>] \
      [vwn_2 <real prefactor default 1.0>] \
      [vwn_3 <real prefactor default 1.0>] \
      [vwn_4 <real prefactor default 1.0>] \
      [vwn_5 <real prefactor default 1.0>] \
      [vwn_1_rpa <real prefactor default 1.0>]]

The user has the option of specifying the exchange-correlation treatment in the DFT Module (see table 11.1). The default exchange-correlation functional is defined as the local density approximation (LDA) for closed shell systems and its counterpart the local spin-density (LSD) approximation for open shell systems. Within this approximation the exchange functional is the Slater $\rho^{1/3}$ functional (from J.C. Slater, Quantum Theory of Molecules and Solids, Vol. 4: The Self-Consistent Field for Molecules and Solids (McGraw-Hill, New York, 1974)), and the correlation functional is the Vosko-Wilk-Nusair (VWN) functional (functional V) (S.J. Vosko, L. Wilk and M. Nusair, Can. J. Phys. 58, 1200 (1980)). The parameters used in this formula are obtained by fitting to the Ceperley and Alder^11.2Quantum Monte-Carlo solution of the homogeneous electron gas.

These defaults can be invoked explicitly by specifying the following keywords within the DFT module input directive, XC slater vwn_5.

That is, this statement in the input file

dft
  XC slater vwn_5
end
task dft

is equivalent to the simple line

task dft

The DECOMP directive causes the components of the energy corresponding to each functional to be printed, rather than just the total exchange-correlation energy which is the default. You can see an example of this directive in the sample input in Section 11.4.

Many alternative exchange and correlation functionals are available to the user as listed in table 11.1. The following sections describe how to use these options.

11.3.1 Exchange-Correlation Functionals

There are several Exchange and Correlation functionals in addition to the default slater and vwn_5 functionals. These are either local or gradient-corrected functionals (GCA); a full list can be found in table 11.1.

The Hartree-Fock exact exchange functional, (which has $O(N^4)$ computation expense), is invoked by specifying

   XC HFexch

Note that the user also has the ability to include only the local or nonlocal contributions of a given functional. In addition the user can specify a multiplicative prefactor (the variable <prefactor> in the input) for the local/nonlocal component or total. An example of this might be,

   XC becke88 nonlocal 0.72

The user should be aware that the Becke88 local component is simply the Slater exchange and should be input as such.

Any combination of the supported exchange functional options can be used. For example the popular Gaussian B3 exchange could be specified as:

   XC slater 0.8 becke88 nonlocal 0.72 HFexch 0.2

Any combination of the supported correlation functional options can be used. For example B3LYP could be specified as:

XC vwn_1_rpa 0.19 lyp 0.81 HFexch 0.20  slater 0.80 becke88 nonlocal 0.72

11.3.2 Combined Exchange and Correlation Functionals

In addition to the options listed above for the exchange and correlation functionals, the user has the alternative of specifying combined exchange and correlation functionals. A complete list of the available functionals appears in table 11.1.

The available hybrid functionals (where a Hartree-Fock Exchange component is present) consist of the Becke ``half and half'' (see A.D. Becke, J. Chem. Phys. 98, 1372 (1992)), the adiabatic connection method (see A.D. Becke, J. Chem. Phys. 98, 5648 (1993)), B3LYP (popularized by Gaussian9X), Becke 1997 (``Becke V'' paper: A.D.Becke, J. Chem. Phys., 107, 8554 (1997)).

The keyword beckehandh specifies that the exchange-correlation energy will be computed as

$$\begin{eqnarray*} E_{XC} \ \approx \ \frac{1}{2} E^{\rm HF}_X + \frac{1}{2} E^{\rm Slater}_{X} + \frac{1}{2} E^{\rm PW91LDA}_{C} \end{eqnarray*}$$

We know this is NOT the correct Becke prescribed implementation which requires the XC potential in the energy expression. But this is what is currently implemented as an approximation to it.

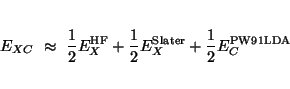
The keyword acm specifies that the exchange-correlation energy is computed as

$$\begin{eqnarray*} E_{XC} \ &=& \ a_0 E^{\rm HF}_X + (1-a_0) E^{\rm Slater}_{X} +... ...\\ & &{\rm where } \\ a_0 &=& 0.20, \ a_X = 0.72, \ a_C = 0.81 \end{eqnarray*}$$

and $\Delta$ stands for a non-local component.

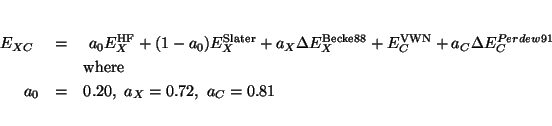
The keyword b3lyp specifies that the exchange-correlation energy is computed as

$$\begin{eqnarray*} E_{XC} \ &=& \ a_0 E^{\rm HF}_X + (1-a_0) E^{\rm Slater}_{X} +... ...\\ & &{\rm where } \\ a_0 &=& 0.20, \ a_X = 0.72, \ a_C = 0.81 \end{eqnarray*}$$

11.3.3 Meta-GGA Functionals

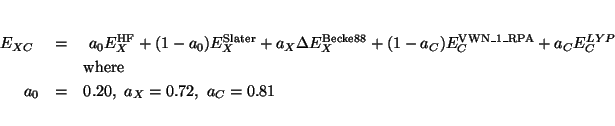
One way to calculate meta-GGA energies is to use orbitals and densities from fully self-consistent GGA or LDA calculations and run them in one iteration in the meta-GGA functional. It is expected that meta-GGA energies obtained this way will be close to fully self consistent meta-GGA calculations. This can be easily accomplished in NWChem, and is our current implementation, which is illustrated in the example below.

This kind of calculation will obviously not converge the energy. To avoid an error in the standard Unix output of NWChem, you must tell NWChem to ignore the returned result of the task, which may be accomplished in the input file with task dft ignore You may still get a warning in the output to the effect, !! warning: dft energy failed. This simply means the energy failed to converge since you ran only one iteration of the functional.

(For more information, see S. Kurth, J. Perdew, P. Blaha, Int. J. Quant. Chem 75, 889 (1999) for a brief description of meta-GGAs, and citations 14-27 therein for thorough background )

11.4 Sample input file

A simple example calculates the meta-GGA exchange energy of water, using converged GGA orbitals and densities to evaluate the meta-GGA energy functional, and also highlights some of the print features in the DFT module:

title "WATER 6-311G* meta-GGA X with PBE orbitals"
echo
geometry units angstroms
  O       0.0  0.0  0.0
  H       0.0  0.0  1.0
  H       0.0  1.0  0.0
end

basis
  H library 6-311G*
  O library 6-311G*
end
 
dft
 print low kinetic_energy
 xc xpbe96 cpbe96
 decomp
end
task dft optimize


dft
 iterations 1
 xc xpkzb99
 decomp
 print low quadrature kinetic_energy
end
task dft ignore

Below are the results of the exchange-only meta-GGA calculation part, and as expected we are reminded the calculation was not allowed to converge:

      Calculation failed to converge
      ------------------------------

         Total DFT energy =    -75.948526603774
      One electron energy =   -122.899234375708
           Coulomb energy =     46.745269703266
          Exchange energy =     -8.857824284365
       Correlation energy =      0.000000000000
 Nuclear repulsion energy =      9.063262353032

 Numeric. integr. density =     10.000001055407

Table 11.1: Table of available Exchange (X) and Correlation (C) functionals. GGA is the Generalized Gradient Approximation, and meta refers to Meta-GGAs. The column 2nds refers to second derivatives of the energy with respect to nuclear position.

Keyword	X	C	GGA	meta	Hybrid	2nds	Ref.
slater	$\star$					Y	[1]
vwn_1		$\star$				Y	[2]
vwn_2		$\star$				Y	[2]
vwn_3		$\star$				Y	[2]
vwn_4		$\star$				Y	[2]
vwn_5		$\star$				Y	[2]
vwn_1_rpa		$\star$				Y	[2]
perdew81		$\star$				Y	[3]
pw91lda		$\star$				Y	[4]
becke88	$\star$		$\star$			Y	[5]
xperdew91	$\star$		$\star$			Y	[6]
xpbe96	$\star$		$\star$			Y	[7]
gill96	$\star$		$\star$			Y	[8]
optx	$\star$		$\star$			N	[20]
mpw91	$\star$		$\star$			Y	[23]
xft97	$\star$		$\star$			N	[24]
perdew86		$\star$	$\star$			Y	[9]
lyp		$\star$	$\star$			Y	[10]
perdew91		$\star$	$\star$			Y	[6]
cpbe96		$\star$	$\star$			Y	[7]
cft97		$\star$	$\star$			N	[25]
hcth	$\star$	$\star$	$\star$			N	[11]
hcth120	$\star$	$\star$	$\star$			N	[12]
hcth147	$\star$	$\star$	$\star$			N	[12]
hcth407	$\star$	$\star$	$\star$			N	[19]
becke97gga1	$\star$	$\star$	$\star$			N	[18]
hcthp14	$\star$	$\star$	$\star$			N	[21]
ft97	$\star$	$\star$	$\star$			N	[24,25]
xpkzb99	$\star$			$\star$		N	[27]
beckehandh	$\star$	$\star$			$\star$	Y	[13]
b3lyp	$\star$	$\star$	$\star$		$\star$	Y	[14]
acm	$\star$	$\star$	$\star$		$\star$	Y	[14]
becke97	$\star$	$\star$	$\star$		$\star$	N	[15]
becke97-1	$\star$	$\star$	$\star$		$\star$	N	[15]
becke97-2	$\star$	$\star$	$\star$		$\star$	N	[22]
becke98	$\star$	$\star$	$\star$		$\star$	N	[16]
pbe0	$\star$	$\star$	$\star$		$\star$	Y	[17]
mpw1k	$\star$	$\star$	$\star$		$\star$	Y	[26]

1. C. Slater, Quantum Theory of Molecules and Solids, Vol. 4 (McGraw-Hill, New York, 1974)
   
2. S.J. Vosko, L. Wilk and M. Nusair, Can. J. Phys. 58, 1200 (1980).
   
3. J. P. Perdew and A. Zunger, Phys. Rev. B 23, 5048 (1981).
   
4. J.P. Perdew and Y. Wang, Phys. Rev. B 45, 13244 (1992).
   
5. A.D. Becke, Phys. Rev. A 88, 3098 (1988).
   
6. J.P. Perdew, J.A. Chevary, S.H. Vosko, K.A. Jackson, M.R. Pederson, D.J. Singh and C. Fiolhais, Phys. Rev. B 46, 6671 (1992).
   
7. J.P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett. 77, 3865 (1996); 78 , 1396 (1997).
   
8. P.W.Gill , Mol. Phys. 89, 433 (1996).
   
9. J. P. Perdew, Phys. Rev. B 33, 8822 (1986).
   
10. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B 37, 785 (1988).
    
11. F.A.Hamprecht, A.J.Cohen, D.J.Tozer and N.C.
    Handy, J. Chem. Phys. 109, 6264 (1998).
    
12. A.D.Boese, N.L.Doltsinis, N.C.Handy and M.Sprik. J. Chem. Phys. 112, 1670 (2000).
    
13. A.D. Becke, J. Chem. Phys. 98, 1372 (1992).
    
14. A.D. Becke, J. Chem. Phys. 98, 5648 (1993).
    
15. A.D.Becke, J. Chem. Phys. 107, 8554 (1997).
    
16. H.L.Schmider and A.D. Becke, J. Chem. Phys. 108, 9624 (1998).
    
17. C.Adamo and V.Barone, J. Chem. Phys. 110, 6158 (1998).
    
18. A.J.Cohen and N.C. Handy, Chem. Phys. Lett. 316, 160 (2000).
    
19. A.D.Boese, N.C.Handy, J. Chem. Phys. 114, 5497 (2001).
    
20. N.C.Handy, A.J. Cohen, Mol. Phys. 99, 403 (2001).
    
21. G. Menconi, P.J. Wilson, D.J. Tozer, J. Chem. Phys 114, 3958 (2001).
    
22. P.J. Wilson, T.J. Bradley, D.J. Tozer, J. Chem. Phys 115, 9233 (2001).
    
23. C. Adamo and V. Barone, J. Chem. Phys. 108, 664 (1998).
    
24. M.Filatov and W.Thiel, Mol.Phys. 91, 847 (1997).
    
25. M.Filatov and W.Thiel, Int.J.Quantum Chem. 62, 603 (1997).
    
26. B.J.Lynch, P.L.Fast, M.Harris and D.G.Truhlar, J. Phys. Chem. A 104, 4811(2000).
    
27. J.P. Perdew, S. Kurth, A. Zupan and P. Blaha, Phys. Rev. Lett. 82, 2544 (1999)
    

11.5 ITERATIONS -- Number of SCF iterations

  ITERATIONS <integer iterations default 30>

The default optimization in the DFT module is to iterate on the Kohn-Sham (SCF) equations for a specified number of iterations (default 30). The keyword that controls this optimization is ITERATIONS, and has the following general form,

   iterations <integer iterations default 30>

The optimization procedure will stop when the specified number of iterations is reached or convergence is met. See an example that uses this directive in section 11.4.

11.6 CONVERGENCE -- SCF Convergence Control

  CONVERGENCE [energy <real energy default 1e-6>] \
              [density <real density default 1e-5>] \
              [gradient <real gradient default 5e-4>] \
              [hl_tol <real hl_tol default 0.1>]
              [dampon <real dampon default 0.0>] \
              [dampoff <real dampoff default 0.0>] \
              [ncydp <integer ncydp default 2>] \
              [ncyds <integer ncyds default 30>] \
              [ncysh <integer ncysh default 30>] \
              [damp <integer ndamp default 0>] [nodamping] \
              [diison <real diison default 0.0>] \
              [diisoff <real diisoff default 0.0>] \
              [(diis [nfock <integer nfock default 10>]) || nodiis] \
              [levlon <real levlon default 0.0>] \
              [levloff <real levloff default 0.0>] \
              [(lshift <real lshift default 0.5>) || nolevelshifting] \
              [rabuck [n_rabuck <integer n_rabuck default 25>]]

Convergence is satisfied by meeting any or all of three criteria;

• convergence of the total energy; this is defined to be when the total DFT energy at iteration N and at iteration N-1 differ by a value less than some value (the default is 1e-6). This value can be modified using the key word,

    CONVERGENCE energy <real energy default 1e-6>
  

• convergence of the total density; this is defined to be when the total DFT density matrix at iteration N and at iteration N-1 have a RMS difference less than some value (the default is 1e-5). This value can be modified using the key word,

    CONVERGENCE density <real density default 1e-5>
  

• convergence of the orbital gradient; this is defined to be when the DIIS error vector becomes less than some value (the default is 5e-4). This value can be modified using the key word,

    CONVERGENCE gradient <real gradient default 5e-4>
  

The default optimization strategy is to immediately begin direct inversion of the iterative subspace^11.3. Damping is also initiated (using 70% of the previous density) for the first 2 iteration. In addition, if the HOMO - LUMO gap is small and the Fock matrix somewhat diagonally dominant, then level-shifting is automatically initiated. There are a variety of ways to customize this procedure to whatever is desired.

An alternative optimization strategy is to specify, by using the change in total energy (from iterations when N and N-1), when to turn damping, level-shifting, and/or DIIS on/off. Start and stop keywords for each of these is available as,

  CONVERGENCE  [dampon <real dampon default 0.0>] \
               [dampoff <real dampoff default 0.0>] \
               [diison <real diison default 0.0>] \
               [diisoff <real diisoff default 0.0>] \
               [levlon <real levlon default 0.0>] \
               [levloff <real levloff default 0.0>]

So, for example, damping, DIIS, and/or level-shifting can be turned on/off as desired.

Another strategy can be to simply specify how many iterations (cycles) you wish each type of procedure to be used. The necessary keywords to control the number of damping cycles (ncydp), the number of DIIS cycles (ncyds), and the number of level-shifting cycles (ncysh) are input as,

  CONVERGENCE  [ncydp <integer ncydp default 2>] \
               [ncyds <integer ncyds default 30>] \
               [ncysh <integer ncysh default 0>]

The amount of damping, level-shifting, time at which level-shifting is automatically imposed, and Fock matrices used in the DIIS extrapolation can be modified by the following keywords

  CONVERGENCE  [damp <integer ndamp default 0>] \
               [diis [nfock <integer nfock default 10>]] \
               [lshift <real lshift default 0.5>] \
               [hl_tol <real hl_tol default 0.1>]]

Damping is defined to be the percentage of the previous iterations density mixed with the current iterations density. So, for example

  CONVERGENCE damp 70

would mix 30% of the current iteration density with 70% of the previous iteration density.

Level-Shifting^11.4 is defined as the amount of shift applied to the diagonal elements of the unoccupied block of the Fock matrix. The shift is specified by the keyword lshift. For example the directive,

  CONVERGENCE lshift 0.5

causes the diagonal elements of the Fock matrix corresponding to the virtual orbitals to be shifted by 0.5 a.u. By default, this level-shifting procedure is switched on whenever the HOMO-LUMO gap is small. Small is defined by default to be 0.05 au but can be modified by the directive hl_tol. An example of changing the HOMO-LUMO gap tolerance to 0.01 would be,

  CONVERGENCE hl_tol 0.01

Direct inversion of the iterative subspace with extrapolation of up to 10 Fock matrices is a default optimization procedure. For large molecular systems the amount of available memory may preclude the ability to store this number of N**2 arrays in global memory. The user may then specify the number of Fock matrices to be used in the extrapolation (must be greater than three (3) to be effective). To set the number of Fock matrices stored and used in the extrapolation procedure to 3 would take the form,

  CONVERGENCE diis 3

The user has the ability to simply turn off any optimization procedures deemed undesirable with the obvious keywords,

  CONVERGENCE [nodamping] [nodiis] [nolevelshifting]

For systems where the initial guess is very poor, the user can try the method described in ^11.5that makes use of fractional occupation of the orbital levels during the initial cycles of the SCF convergence. The input has the following form

  CONVERGENCE rabuck [n_rabuck <integer n_rabuck default 25>]]

where the optional value n_rabuck determines the number of SCF cycles during which the method will be active. For example, to set equal to 30 the number of cycles where the Rabuck method is active, you need to use the following line

  CONVERGENCE rabuck 30

11.7 SMEAR -- Fractional Occupation of the Molecular Orbitals

The SMEAR keyword is useful in cases with many degenerate states near the HOMO (eg metallic clusters)

  SMEAR <real smear default 0.001>

This option allows fractional occupation of the molecular orbitals. A Gaussian broadening function of exponent smear is used as described in the paper: R.W. Warren RW and B.I. Dunlap, Chem. Phys. Letters 262, 384 (1996).
The user must be aware that an additional energy term is added to the total energy in order to have energies and gradients consistent.

11.8 GRID -- Numerical Integration of the XC Potential

  GRID [(xcoarse||coarse||medium||fine||xfine) default medium] \
       [(gausleg||lebedev ) default lebedev ] \
       [(old||new) default new ] \
       [(becke||erf1||erf2||ssf) default erf1] \
       [(euler||mura||treutler) default mura] \
       [rm <real rm default 2.0>]

A numerical integration is necessary for the evaluation of the exchange-correlation contribution to the density functional. The default quadrature used for the numerical integration is an Euler-MacLaurin scheme for the radial components (with a modified Mura-Knowles transformation) and a Lebedev scheme for the angular components. Within this numerical integration procedure various levels of accuracy have been defined and are available to the user. The user can specify the level of accuracy with the keywords; xcoarse, coarse, medium, fine, and xfine. The default is medium.

  GRID [xcoarse||coarse||medium||fine||xfine]

Our intent is to have a numerical integration scheme which would give us approximately the accuracy defined below regardless of molecular composition.

Keyword	Total Energy Target Accuracy
xcoarse	$1x10^{-4}$
coarse	$1x10^{-5}$
medium	$1x10^{-6}$
fine	$1x10^{-7}$
xfine	$1x10^{-8}$

In order to determine the level of radial and angular quadrature needed to give us the target accuracy we computed total DFT energies at the LDA level of theory for many homonuclear atomic, diatomic and triatomic systems in rows 1-4 of the periodic table. In each case all bond lengths were set to twice the Bragg-Slater radius. The total DFT energy of the system was computed using the converged SCF density with atoms having radial shells ranging from 35-235 (at fixed 48/96 angular quadratures) and angular quadratures of 12/24-48/96 (at fixed 235 radial shells). The error of the numerical integration was determined by comparison to a ``best'' or most accurate calculation in which a grid of 235 radial points 48 theta and 96 phi angular points on each atom was used. This corresponds to approximately 1 million points per atom. The following tables were empirically determined to give the desired target accuracy for DFT total energies. These tables below show the number of radial and angular shells which the DFT module will use for for a given atom depending on the row it is in (in the periodic table) and the desired accuracy. Note, differing atom types in a given molecular system will most likely have differing associated numerical grids. The intent is to generate the desired energy accuracy (with utter disregard for speed).

Table 11.2: Program default number of radial and angular shells empirically determined for Row 1 atoms (Li $\rightarrow$ F) to reach the desired accuracies.

Keyword	Radial	Angular
xcoarse	21	194
coarse	35	302
medium	49	434
fine	70	590
xfine	100	1202

Table 11.3: Program default number of radial and angular shells empirically determined for Row 2 atoms (Na $\rightarrow$ Cl) to reach the desired accuracies.

Keyword	Radial	Angular
xcoarse	42	194
coarse	70	302
medium	88	434
fine	123	770
xfine	125	1454

Table 11.4: Program default number of radial and angular shells empirically determined for Row 3 atoms (K $\rightarrow$ Br) to reach the desired accuracies.

Keyword	Radial	Angular
xcoarse	75	194
coarse	95	302
medium	112	590
fine	130	974
xfine	160	1454

Table 11.5: Program default number of radial and angular shells empirically determined for Row 4 atoms (Rb $\rightarrow$ I) to reach the desired accuracies.

Keyword	Radial	Angular
xcoarse	84	194
coarse	104	302
medium	123	590
fine	141	974
xfine	205	1454

11.8.1 Angular grids

In addition to the simple keyword specifying the desired accuracy as described above, the user has the option of specifying a custom quadrature of this type in which ALL atoms have the same grid specification. This is accomplished by using the gausleg keyword.

11.8.1.0.1 Gauss-Legendre angular grid

  GRID gausleg <integer nradpts default 50> <integer nagrid default 10>

In this type of grid, the number of phi points is twice the number of theta points. So, for example, a specification of,

  GRID gausleg 80 20

would be interpreted as 80 radial points, 20 theta points, and 40 phi points per center (or 64000 points per center before pruning).

11.8.1.0.2 Lebedev angular grid

A second quadrature is the Lebedev scheme for the angular components^11.6. Within this numerical integration procedure various levels of accuracy have also been defined and are available to the user. The input for this type of grid takes the form,

  GRID lebedev <integer radpts > <integer iangquad >

In this context the variable iangquad specifies a certain number of angular points as indicated by the table below.^11.7

Table 11.6: List of Lebedev quadratures

$IANGQUAD$	$N_{angular}$	$l$
1	38	9
2	50	11
3	74	13
4	86	15
5	110	17
6	146	19
7	170	21
8	194	23
9	230	25
10	266	27
11	302	29
12	350	31
13	434	35
14	590	41
15	770	47
16	974	53
17	1202	59
18	1454	65
19	1730	71
20	2030	77
21	2354	83
22	2702	89
23	3074	95
24	3470	101
25	3890	107
26	4334	113
27	4802	119
28	5294	125
29	5810	131

Therefore the user can specify any number of radial points along with the level of angular quadrature (1-29).

The user can also specify grid parameters specific for a given atom type: parameters that must be supplied are: atom tag and number of radial points. As an example, here is a grid input line for the water molecule

grid lebedev 80 11 H 70 8  O 90 11

11.8.2 Partitioning functions

  GRID [(becke||erf1||erf2||ssf) default erf1]

becke

A. D. Becke, J. Chem. Phys. 88, 1053 (1988).

ssf

R.E.Stratmann, G.Scuseria and M.J.Frisch, Chem. Phys. Lett. 257, 213 (1996).

erf1

modified ssf

erf2

modified ssf

Erf$n$ partioning functions

$$\begin{eqnarray*} w_A(r) & = & \prod_{B\neq A}\frac{1}{2} \left[1 \ - \ erf(\mu... ...thbf r}_B} {\left\vert{\mathbf r}_A - {\mathbf r}_B \right\vert} \end{eqnarray*}$$

11.8.3 Radial grids

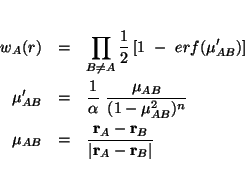
  GRID [[euler||mura||treutler]  default mura]

euler

Euler-McLaurin quadrature wih the transformation devised by C.W. Murray, N.C. Handy, and G.L. Laming, Mol. Phys.78, 997 (1993).

mura

Modification of the Murray-Handy-Laming scheme by M.E.Mura and P.J.Knowles, J Chem Phys 104, 9848 (1996) (we are not using the scaling factors proposed in this paper).

treutler

Gauss-Chebyshev using the transformation suggested by O.Treutler and R.Alrhichs, J.Chem.Phys 102, 346 (1995).

11.8.4 Grid Scheme

  GRID [[old||new]  default new]

In NWChem 4.0 the XC integration code has been re-written using a space decomposiition scheme similar to the one proposed in R.E.Stratmann, G.Scuseria and M.J.Frisch, Chem. Phys. Lett. 257, 213 (1996) (keyword new).

To use the XC integration routines available in older version of NWChem, use the keyword old.

11.9 TOLERANCES -- Screening tolerances

  TOLERANCES [[tight] [tol_rho <real tol_rho default 1e-10>] \
              [accCoul <integer accCoul default 8>] \
              [radius <real radius default 25.0>]]

The user has the option of controlling screening for the tolerances in the integral evaluations for the DFT module. In most applications, the default values will be adequate for the calculation, but different values can be specified in the input for the DFT module using the keywords described below.

The input parameter accCoul is used to define the tolerance in Schwarz screening for the Coulomb integrals. Only integrals with estimated values greater than $10^{(-{\tt accCoul})}$ are evaluated.

  TOLERANCES accCoul <integer accCoul default 8>

Screening away needless computation of the XC functional (on the grid) due to negligible density is also possible with the use of,

  TOLERANCES tol_rho <real tol_rho default 1e-10>

XC functional computation is bypassed if the corresponding density elements are less than tol_rho.

A screening parameter, radius, used in the screening of the Becke or Delley spatial weights is also available as,

  TOLERANCES radius <real radius default 25.0>

where radius is the cutoff value in bohr.

The tolerances as discussed previously are insured at convergence. More sleazy tolerances are invoked early in the iterative process which can speed things up a bit. This can also be problematic at times because it introduces a discontinuity in the convergence process. To avoid use of initial sleazy tolerances the user can invoke the tight option:

  TOLERANCES tight

This option sets all tolerances to their default/user specified values at the very first iteration.

11.10 DIRECT and NOIO -- Hardware Resource Control

  DIRECT||INCORE
  NOIO

The inverted charge-density and exchange-correlation matrices for a DFT calculation are normally written to disk storage. The user can prevent this by specifying the keyword noio within the input for the DFT directive. The input to exercise this option is as follows,

   noio

If this keyword is encountered, then the two matrices (inverted charge-density and exchange-correlation) are computed ``on-the-fly'' whenever needed.

The INCORE option is always assumed to be true but can be overridden with the option DIRECT in which case all integrals are computed ``on-the-fly''.

11.11 ODFT and MULT -- Open shell systems

  ODFT
  MULT <integer mult default 1>

Both closed-shell and open-shell systems can be studied using the DFT module. Specifying the keyword MULT within the DFT directive allows the user to define the spin multiplicity of the system. The form of the input line is as follows;

   MULT <integer mult default 1>

When the keyword MULT is specified, the user can define the integer variable mult, where mult is equal to the number of alpha electrons minus beta electrons, plus 1.

The keyword ODFT is unnecessary except in the context of forcing a singlet system to be computed as an open shell system (i.e., using a spin-unrestricted wavefunction).

11.12 SIC -- Self-Interaction Correction

sic [perturbative || oep || oep-loc <default perturbative>]

The Perdew and Zunger (see J. P. Perdew and A. Zunger, Phys. Rev. B 23, 5048 (1981)) method to remove the self-interaction contained in many exchange-correlation functionals has been implemented with the Optimized Effective Potential method (see R. T. Sharp and G. K. Horton, Phys. Rev. 90, 317 (1953), J. D. Talman and W. F. Shadwick, Phys. Rev. A 14, 36 (1976)) within the Krieger-Li-Iafrate approximation (J. B. Krieger, Y. Li, and G. J. Iafrate, Phys. Rev. A 45, 101 (1992); 46, 5453 (1992); 47, 165 (1993)) Three variants of these methods are included in NWChem:

• sic perturbative This is the default option for the sic directive. After a self-consistent calculation, the Kohn-Sham orbitals are localized with the Foster-Boys algorithm (see section 10.15) and the self-interaction energy is added to the total energy. All exchange-correlation functionals implemented in the NWChem can be used with this option.
• sic oep With this option the optimized effective potential is built in each step of the self-consistent process. Because the electrostatic potential generated for each orbital involves a numerical integration, this method can be expensive.
• sic oep-loc This option is similar to the oep option with the addition of localization of the Kohn-Sham orbitals in each step of the self-consistent process.

With oep and oep-loc options a xfine grid (see section 11.8) must be used in order to avoid numerical noise, furthermore the hybrid functionals can not be used with these options. More details of the implementation of this method can be found in J. Garza, J. A. Nichols and D. A. Dixon, J. Chem. Phys. 112, 7880 (2000). The components of the sic energy can be printed out using:

print "SIC information"

11.13 MULLIKEN -- Mulliken analysis

Mulliken analysis of the charge distribution is invoked by the keyword:

  MULLIKEN

When this keyword is encountered, Mulliken analysis of both the input density as well as the output density will occur. For example, to perform a mulliken analysis and print the explicit population analysis of the basis functions, use the following

dft
 mulliken
 print "mulliken ao"
end
task dft

11.14 BSSE -- Basis Set Superposition Error

Particular care is required to compute BSSE by the counter-poise method for the DFT module. In order to include terms deriving from the numerical grid used in the XC integration, the user must label the ghost atoms not just bq, but bq followed by the given atomic symbol. For example, the first component needed to compute the BSSE for the water dimer, should be written as follows

geometry h2o autosym units au
 O        0.00000000     0.00000000     0.22143139
 H        1.43042868     0.00000000    -0.88572555
 H       -1.43042868     0.00000000    -0.88572555
 bqH      0.71521434     0.00000000    -0.33214708
 bqH     -0.71521434     0.00000000    -0.33214708
 bqO      0.00000000     0.00000000    -0.88572555
end

basis
 H library aug-cc-pvdz
 O library aug-cc-pvdz
 bqH library H aug-cc-pvdz
 bqO library O aug-cc-pvdz
end

Please note that the ``ghost'' oxygen atom has been labeled bqO, and not just bq.

11.15 Print Control

  PRINT||NOPRINT

The PRINT||NOPRINT options control the level of output in the DFT. Please see some examples using this directive in section 11.4, a sample input file. Known controllable print options are:

Table 11.7: DFT Print Control Specifications

Name	Print Level	Description
``all vector symmetries''	high	symmetries of all molecular orbitals
``alpha partner info''	high	unpaired alpha orbital analysis
``common''	debug	dump of common blocks
``convergence''	default	convergence of SCF procedure
``coulomb fit''	high	fitting electronic charge density
``dft timings''	high
``final vectors''	high
``final vector symmetries''	default	symmetries of final molecular orbitals
``information''	low	general information
``initial vectors''	high
``intermediate energy info''	high
``intermediate evals''	high	intermediate orbital energies
``intermediate fock matrix''	high
``intermediate overlap''	high	overlaps between the alpha and beta sets
``intermediate S2''	high	values of S2
``intermediate vectors''	high	intermediate molecular orbitals
``interm vector symm''	high	symmetries of intermediate orbitals
``io info''	debug	reading from and writing to disk
``kinetic_energy''	high	kinetic energy
``mulliken ao''	high	mulliken atomic orbital population
``multipole''	default	moments of alpha, beta, and nuclear charge densities
``parameters''	default	input parameters
``quadrature''	high	numerical quadrature
``schwarz''	high	integral screening info & stats at completion
``screening parameters''	high	integral accuracies
``semi-direct info''	default	semi direct algorithm